こんにちは、大阪京橋数学塾A4Uの六人部です。
大阪府C問題の中でも特色のある問題をピックアップして実際に解いていこうと思います。
今回は2018年度大問1番の(6)です。
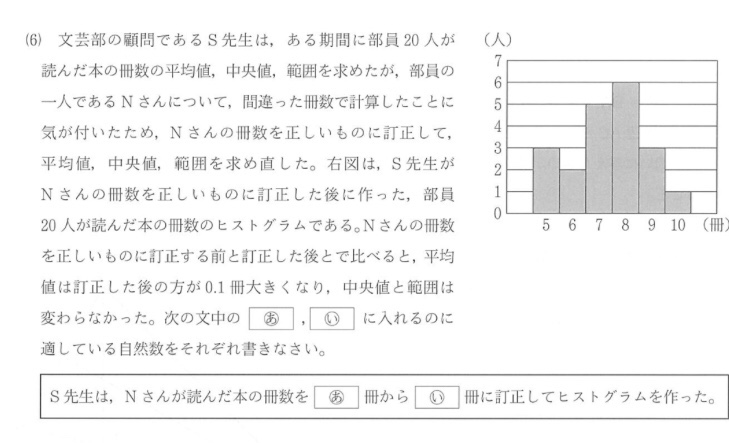
こんな問題。
では、行ってみましょー!
解説
『中央値が変わらなかった』とあるので、訂正は上位10人もしくは下位10人の内部で行われた事が分かります。
平均値が0.1冊大きくなった事から、
0.1×20=2 より
全体の合計が2冊増えた事になります。
(ア)
上位10人のなかで2冊増える訂正は、
8冊→10冊しかあり得ません。
しかし、正しいヒストグラムの10冊の度数は1なので、この訂正があったとすると訂正前の10冊の度数は0だった事になります。
すると、『訂正の前後で範囲が変わらなかった』という条件を満たしません。
(イ)
下位10人の中で2冊増えるような訂正は、
5冊→7冊しかあり得ません。
これは『訂正の前後で範囲が変わらなかった』という条件を満たします。
(ア)(イ)より、
あ=5 い=7 となります。
ポイント
さて、この問題を何故取り上げたかというと『条件による絞り込み』を使って解かなければならないからです。
高校生になると、この手のパターン分けによる考え方は多いのですが、中学生はあまり触れる機会がありません。
そのため、正答率が低くなりがちです。
C問題では条件による絞り込みの問題が良く出題されます。
考えうる可能性を列挙して、1つずつ調べて解として当てはまるものを選ぶ。
これに慣れておきましょう。
条件を満たしていれば解は複数あってもOK。
逆に条件を満たすものが1つも無ければ『解無し』が解となります。
さすがに解無しを問題に出すような意地悪は無いと思いますけどね。
可能性として知っておくのはアリでしょう。
加えてもう1つのポイントとしては『語句の意味はキチンと把握する』ということです。
この問題は『中央値』『範囲』等の語句の意味があやふやだと解けなくなる可能性があります。
自然数、整数、素数、有理数、無理数、挙げるときりがないですが、こういった言葉で引っかかってミスする事がないようにしましょう。
まとめ
C問題の中でも、特徴のある問題を解いてみました。
これからもブログで伝えられる事は記事にしていく予定です。
[getpost id=”945″]

