こんにちは、大阪京橋数学塾A4Uの六人部です。
今回は数学C問題シリーズです。
扱うのは2016年度の大問1(6)
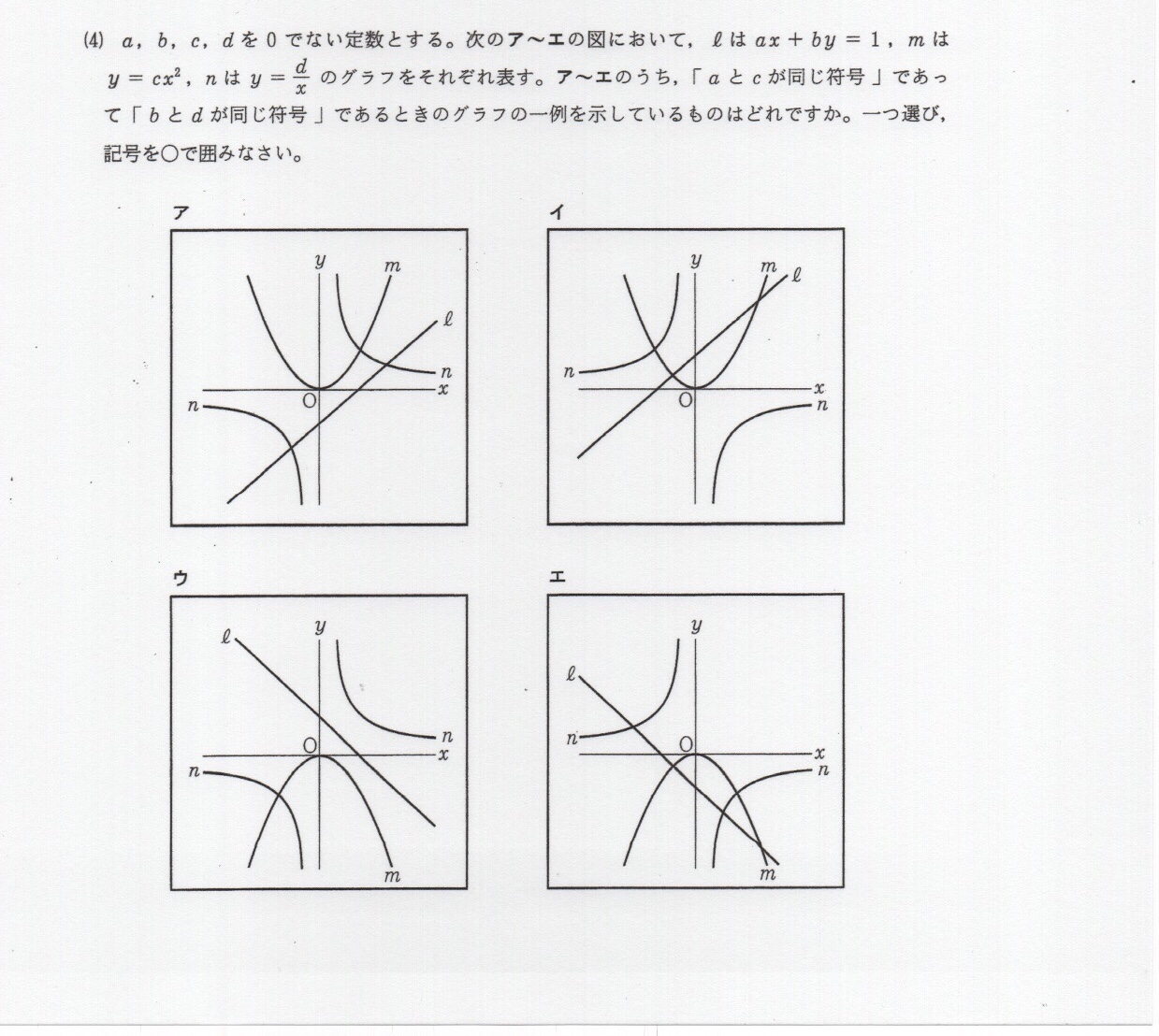
こんな問題です。
この年度は数学C問題導入初年度でして、今までに無かったタイプの問題に苦しんだ受験生も多かったのを記憶しています。
では解いていきましょー!
解法
問題に「aとcが同じ符号」「bとdが同じ符号」とあります。
という事は(aとc,bとd)の正負のパターンは (正,正)、(正,負)、(負,正)、(負,負)の4パターンしかありません。
これらについて1つずつ調べていくのですが、cとdに関しては符号が決まればグラフの形は即座に分かります。
よって、『まず放物線と反比例のグラフの形で該当する選択肢を探し、1次関数のグラフをチェックして条件に合うか確認。』という作業を繰り返していきます。
(正,正)の時
放物線は下に凸、反比例は1,3象限だから該当するのはア。
しかし、このとき1次関数の傾きは負になるので、直線ℓが右上りの直線になっている事からアはハズレ。
(正,負)の時
放物線は下に凸、反比例は2、4象限だから該当するのはイ。
このとき、1次関数の傾きは正になり直線ℓは右上りとなるので合っていそうに見えるが、y切片は負になるのでイもハズレ。
(負,正)の時
放物線は上に凸、反比例は1、3象限だから該当するのはウ。
このとき、1次関数の傾きは正なので直線ℓが右下がりの直線になっている事からウはハズレ。
(負,負)の時
放物線は上に凸、反比例は2、4象限だから該当するのはエ。
このとき、1次関数の傾きは負になり直線ℓは右下がりとなり、y切片も負になっている事からエは条件を満たす。
以上より答えはエとなる。
ちょっと一言
この問題は考えられるパターンが4パターンで選択肢が4つだから全て調べました。
しかし、問題によっては考え得るパターンは8パターンなのに選択肢が4つしか無いような状況もあるかもしれません。
そういう時は選択肢にあるものだけを調べる方が早いので臨機応変に対応しましょう!
まぁ、そういう問題は本質的な理解を問うには向いていないので出ないと思いますがね。
一応注意です。
まとめ
今回は考え得るパターンを考えていき当てはまる図を選択する問題でした。
この問題は正答率も22%と低いです。
適当に選んでも25%になるはずですからキチンと考えられた人は少ないのではないでしょうか!
場合分けの考え方を身につけて、他の受験者に差を付けましょう!

