こんにちは、大阪京橋数学塾A4Uの六人部です。
今回は開明中の入試問題からの紹介です。
基本的な計算ですが、受験生がミスりそうなポイントがあるので取り上げてみました。
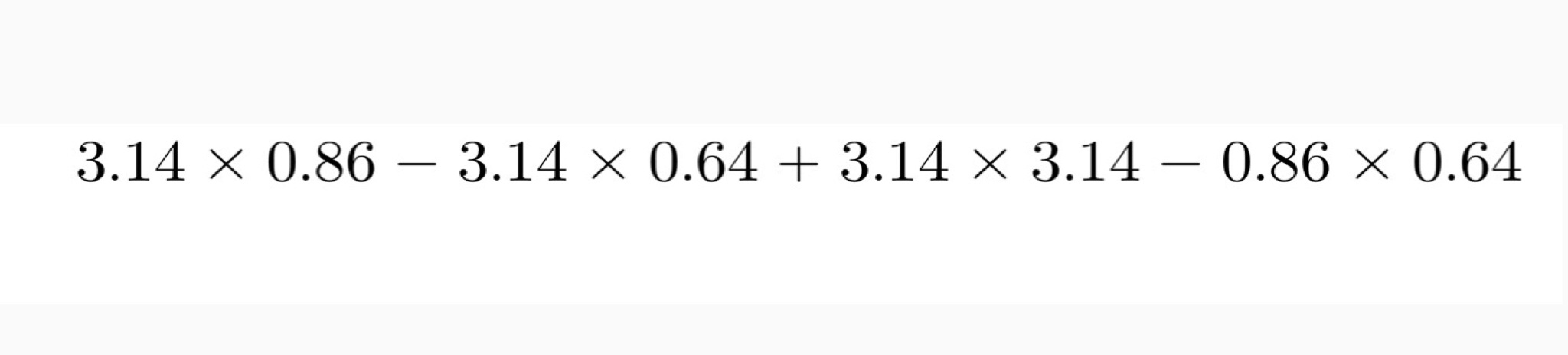
こんな問題です。
さて、では解説いってみましょー。
ミスるパターン
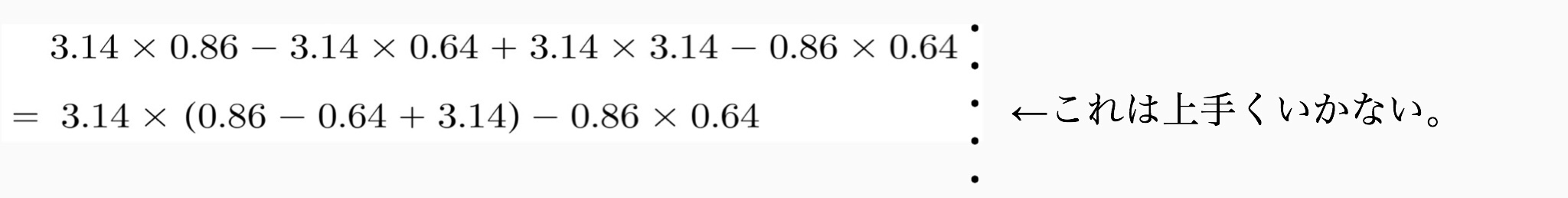
全体を眺めると3.14がいくつもあります。
おっ、3.14でくくれる!
そう思って、くくりに行くとあまり良くないです。
カッコの中身を計算してもあまり綺麗な数字にはなりませんから、お得感が薄いですね。
まぁ、計算力に自信があるならばこれでも正解する事は出来ますが、計算ミスする可能性が高くなります。
何より時間の面でロスが出ます。
後の問題を解く時間を残す観点から、やはり工夫すべきでしょう。
適切な解き方

足し算、引き算は先にまとめておく方が計算が楽になる場合が多い事。
また、その手掛かりとして0.64が2箇所しか無い所に注目しましょう。
すると、どうでしょうか。
その後の式が×4でまとめる事が出来るようになります。
最後は受験生にはお手の物、25×4=100の変化系に落ち着きます。
これなら計算ミスはあまりしないでしょう。
すっきりした計算なので時間もかかりません。
ポイント
受験算数の計算ではこういったスッと解ける問題が必ず入っているので見極められるようになりましょう。
こういった問題に対して、どうしても時間がかかるようなゴリゴリ計算する問題も出るので時間はそういう問題に使いましょう。
大問2番以降をじっくり考える為にも、計算問題をいかに素早く正確に解くかは受験においてポイントです。
まとめ
開明中スーパー理数コースに合格するた為にはかなりの高得点が要求されます。
計算で手間取ってペースを乱されないように、今回のような問題には注意しましょう。
また、工夫して解ける問題と力業で解く問題を見分ける目を養うことも大切です!
■関連記事
≫『開明中学入試データから見える傾向』
≫『続!開明中学入試データ考察』
≫『【開明中過去問】嘘つき問題』
≫『2020年度開明中学出願情報』
≫『開明中学2018年度算数1次後期大問2(5)』

