【中学入試】問題をみて具体例が思いつくか？

こんにちは大阪京橋数学塾A4Uの六人部です。

久方ぶりのブログ更新となってしまいました。。。

春休み明けてから寝ても寝ても眠たい！これが疲労の蓄積か・・・

入試の期間は気が張り詰めていますが春先はどうやらダメなようです。

おっと、話が脱線してしまいました。

今回は入試問題を見て具体例を思いつくことの優位性についてのお話です。

入試問題の解説にちょいとプラスアルファでお話も混ぜてという流れでいこうと思います。

題材は開明中学入試問題です。

どこの問題でも良かったのですが、ちょうど良い問題が目についたので使わせていただきます。

2022開明中学入試算数後期A日程大問3

すぐに解きにかかるという意味合いにおいてね。

もちろん悪い事ではないのですが、この問題を読んだときに頭の中に思い描いて欲しい物があります。

そう、これです。

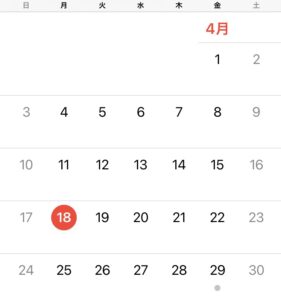
カレンダー。

この問題を読んで「あー、カレンダーね。」と具体物が思いつくかというのは意外に重要です。

何故か？

具体的な物が思い浮かぶと思考が捗るから！

入試において、見たことがある、似たような状況に遭遇したことがある、というのは強烈なアドバンテージです。

特に中学入試では身近なものが題材になる事も多いですから。

日々の生活の中でいろいろな物を見たり聞いたりするのは重要なのです。

問題の状況で何かを想像できるかというのは、ゆくゆくは数式を見てグラフが思い描けるかというような能力に続いていきます。

状況を数式で考える、数式から状況を思い描く。

中学数学、高校数学と乗り切っていくのに必要な能力です。

一方で「問題は問題。」と問題を解くべき対象としてしか考えていないのであればどこかで頭を打つ事になるでしょう。

入試問題にはそういったメッセージも込められていると思うのですが、やはり解説には解き方しか載っていません。

ページ数の関係もあるし、そんなことを語りだしたら長くなるしね。

でも、その解説に載せられない部分こそが超重要であったりするわけなんです。

ですから問題を解く時には必ず「自分が知っている何かと似てないかな？」という感覚で取り組んで欲しいです。

もちろん無けりゃ無いで構わないのです。

考えることが重要です。