こんにちは大阪京橋数学塾A4Uの六人部です。
試験で成績を残すという意識がまだ低い!
生徒達に試験の取り組み方を口うるさく言っているつもりなのですが、まだまだ浸透していないので、こうなったら記事にしてまえ!って事で。
偏差値の計算
まず偏差値、偏差値と言いますがどうやって計算してるんでしょう。

これが偏差値の計算式です。
さてここで、標準偏差ってなんぞ?となるのではないでしょうか。
データのばらつき具合を表す指数とでも考えておいて下さい。
受けた試験によってその都度定まる数値です。
詳しくは高校1年で学習します。
具体例
まぁ文字や公式のまま話を進めても具体的なイメージが湧かないですよね。
そこで、関西圏(特に大阪)でよく使われている五ツ木の模試のデータを使って説明します。
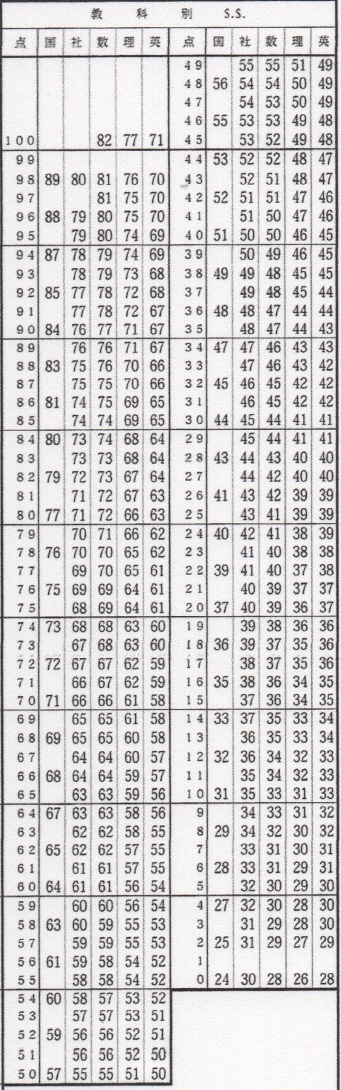
とある回の得点と偏差値(s.s.)の一覧表です。
そうですね、数学のデータでお話しましょう。
この回の数学の平均点は41点で、標準偏差は逆算すると18くらいです。
全ての詳しいデータを持っているわけではないので、標準偏差を正確には計算出来ませんが今回お話したい事に関しては標準偏差は数値であるという事が重要なので、ここは18として計算します。
ここで偏差値をy、得点をx、平均点41、標準偏差18として偏差値の式書き直して整理してみましょう。
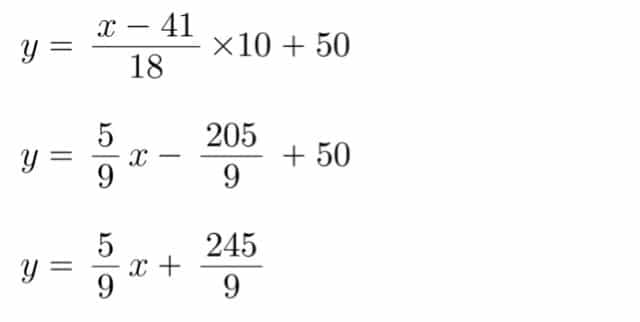
すると、上の式のように偏差値が1次関数で表せました。
つまり偏差値は245/9 = 27.2をスタートにして、得点に応じて上がって行く事が分かります。
1点は1点!
さて何が述べたかったのかというと、偏差値は1次関数的に上がって行く、ここです。
これを伝えたかったんですね。
直線的に上がるんです。
得点にだけ依存して愛もなく無慈悲にです。
つまり計算問題で獲得した点も、難しい図形問題を獲得した点も同価値で扱われるという事です。
1点は1点という世界なんですよ。
よって時間のかかる図形問題などで点を取るならまず計算問題が全問正解で無ければもったいないのです。
いやいや、図形問題の方が配点高いから差が出るでしょ?
そういう意見が出そうです。
そうですね。
確かに差が出そうです。
少し試験の配点についてもお話しましょう。
配点は(4点)× 19問、(2点)×4問、(5点)×2問、(6点)×1問、となっております。
ほとんどが4点であり、計算問題も4点の配点で4問あります。
唯一の配点6点の問題は図形の証明問題。
確かに差がありましたね。
ありましたが、かかる時間から考えれば計算の方が断然おいしいですね。
図形の証明を解く時間があれば計算4問解けますから!
よって、ここがポイントです。
模試で5分かけて切っ掛けさえつかめない問題に出くわしたら、解かなくて良いです。
無視しましょう。
その問題を悩む時間は、
・計算問題の解きなおし
・方程式の問題の検算
・問われた事にキチンと答えられているか?
・単位の間違いはないか?
そういったチェックをして、書けたところを確実に得点にしましょう。
これを徹底すれば偏差値60を切る事は無いですよ!
まとめ
どうもやってる割に成績に繋がらない。
そういう人は試験の取り組み方に問題があるかもしれません。
試験はスポーツで言うならば試合です。
練習で意識すべき事と試合で意識すべき事は当然違ってきます。
結果を残す事を意識して試験に取り組みましょう!

