こんにちは、大阪京橋数学塾A4Uの六人部です。
今回は大阪府の公立高校入試直前という事で図形問題のちょっとしたコツをお伝えします。
こうすれば解ける!という程のものではないですが、忘れやすい図形の知識などを押さえておきましょう。
逆を忘れがちな法則
直角三角形の外接円
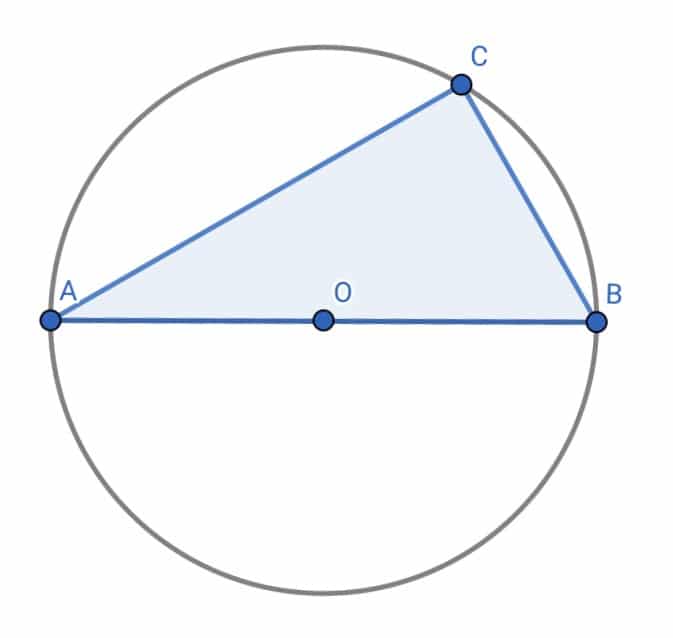
上の図の様に円の直径を含む円に内接する三角形は直角三角形です!
これは直径に対する円周角と中心角の関係から明らかですね。
これに気づける人は多いのに、逆を見逃す人は非常に多いです。
直角三角形があれば斜辺の中点を中心とする外接円がかける。という事!
書いた円が問題を解く手がかりになる事は多く、特にAO=BO=COの関係から二等辺三角形を見抜くなどは頻出です。
四角形の外接円
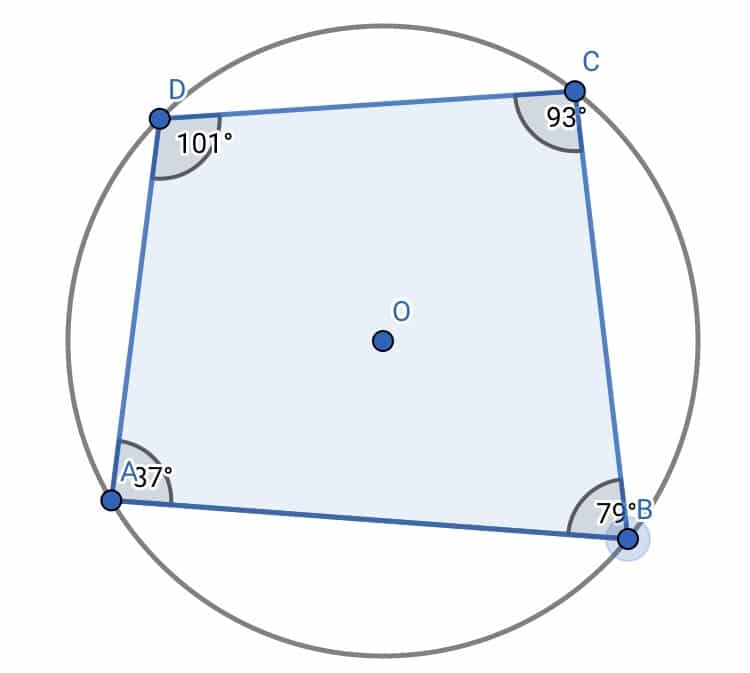
上の図のような円に内接する四角形は向かい合う角の和が180°になります。
これも円周角の関係から言える事ですね。
円が書いてある状態でなら気づくのですが、向かい合う角の和が180°である四角形だけ書いてある場合に円の存在をスルーしてしまいがちです。
この円の存在に気づき、円周角で攻めて行くような問題も良く出ます!
角度
角を文字式で表せ。
というような問題は入試でよく出題されますね。
この手の問題で忘れやすいのが合同や相似を使って等しい角を見つける事です。
大抵の場合、そうやって発想する問題は手前で合同や相似の証明をやらされていたりして誘導が入っているので気づける事もあります。
やっかいなのは単発の角度の問題でそうした発想を要する問題ですね。
合同や相似を使うかもしれない!と頭の片隅に意識しておきましょう。
そうでないと見逃しますよ。
補助線
これは忘れやすい訳ではありませんが、補助線とかどこに引けばいいか分からん!といった人が多いと思うのでお話します。
補助線を引く時のポイント。
それは平行線です!
・ある辺に平行な直線を増やす。
・既に存在する平行線を利用するために線分を延長したりして、平行線との交点を増やす。
こういった発想で引きましょう。
闇雲に謎の線を引いてもラッキーは起こりにくいです。
全ての補助線がこれに該当する訳ではありませんが、これくらいを押さえておくだけでも効果は十分だと思います!
まとめ
今回は発想の取っ掛かりになりそうな図形問題のポイントをお伝えしました。
大抵、図形問題の重要なヒントは見えないようにしてあります。
それに気づけるかが正しく勝負の分かれ目です。
見えないものを見ようとしてください!(望遠鏡は担がなくて良いですよ。笑)
最後になりましたが、解けなさそうな図形の問題で最後の5分粘るよりは計算問題を5分使って検算する方がよっぽど重要だという事は忘れないように!
入試まであと少し頑張りましょう!

