こんにちは、大阪京橋数学塾A4Uの六人部です。
今回は2次関数に使える小技を紹介します。
放物線上の2点を通る直線の式をものの数秒で出す方法です。
では、いきます。
グラフ上の2点を通る直線の式
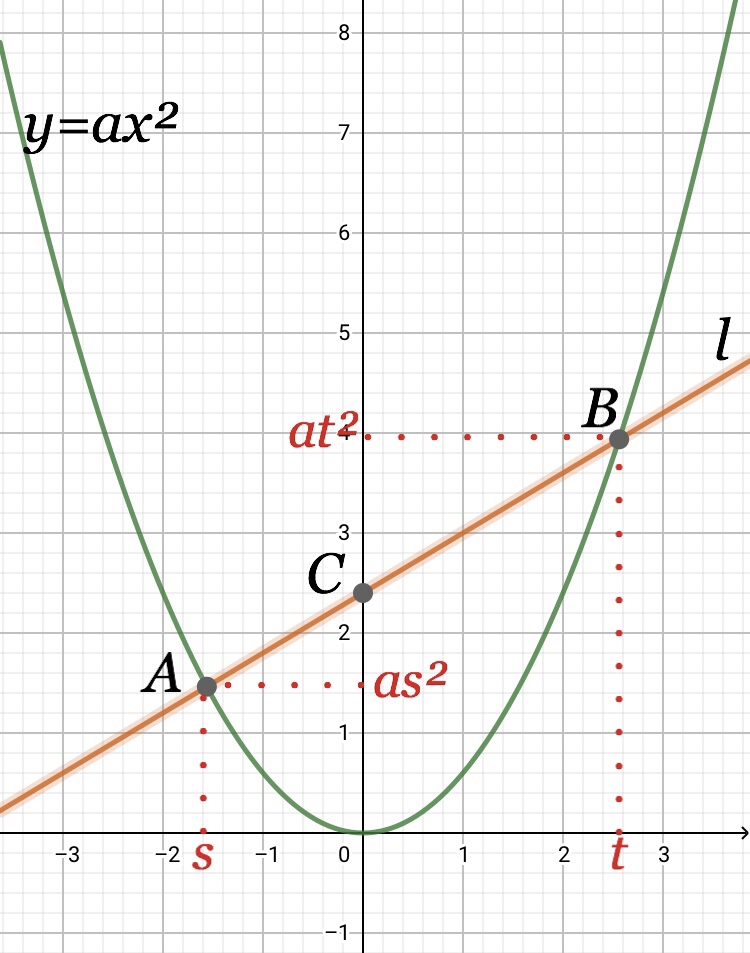
図のようにグラフ上の2点A,Bのx座標をそれぞれs,tとします。
(注)図はa>0の場合ですが、a<0の場合も同様の結果となります。
まず、2点A,Bを通る直線ℓの傾きから考えましょう。
\begin{eqnarray}(傾き)&&=&&(変化の割合)\\[5mm]&&=&&\cfrac{(yの増加量)}{(xの増加量)}\\[5mm]&&=&&\cfrac{at^2-as^2}{t-s}\\[5mm]&&=&&\cfrac{a(t^2-s^2)}{t-s}\\&&=&&\cfrac{a(t+s)(t-s)}{t-s}\\[5mm]&&=&&a(t+s)\\[5mm]&&=&&a(s+t)\\[5mm]&&=&&a\times(2点のx座標の和)\end{eqnarray}
\begin{eqnarray}&&また、直線lの式は切片をbとして、\\[5mm]&&y=a(s+t)x+b と表せる。\\[5mm]&&lは点A(s,as^2)を通るので、\\[5mm]&&as^2=a(s+t)\times s+b\\[5mm]&&したがってb=-ast\end{eqnarray}
\begin{eqnarray}&&よって直線lの式はy=a(s+t)x-astと表せる。\\[5mm]&&つまり以下のことが成り立つ。\end{eqnarray}
\begin{eqnarray}(傾き)&&=&&a\times(2点のx座標の和)\\[5mm](y切片)&&=&&-a\times(2点のx座標の積)\end{eqnarray}
注意点!
上に示した方法はあくまでスピードを重視する場合のやり方であり、本質的な事からは外れています。
よって、記述式の問題の答案に書くには向いていません。
試験でどうしても時間を稼ぎたい場合に使える小技であり、本来なら検算に利用して欲しいものです。
また、こういったテクニックだけ覚えて、何故こうなったのかという部分を忘れては今からの時代の入試には対応できません。(高校の勉強で確実に困ります。)
何故そうなるのかが重要なのです。
技を使うならその理由ごと理解して使いましょう!
まとめ
今回はちょいと使える小技をお伝えしました。
しかし、正攻法が完璧であればこその小技だと僕は考えています。
正攻法で攻めつつ、技も使える!
そんな状態が理想かもしれませんね。
今後も使える小ネタはどんどんアップしますね。