こんにちは、大阪京橋数学塾A4Uの六人部です。
今回は大阪府公立高校入試の数学C問題以外からの問題を紹介します。
工夫が必要な計算問題です。

京都の堀川高校で29年度に出題された問題です。
堀川高校は京都御三家に名を連ねる名門高校の内の1校です。
非常に示唆に富んだ問題です。
では、行ってみよー!
(ア)解説

(イ)解説
(ア)で得た法則で式を書き直すと、
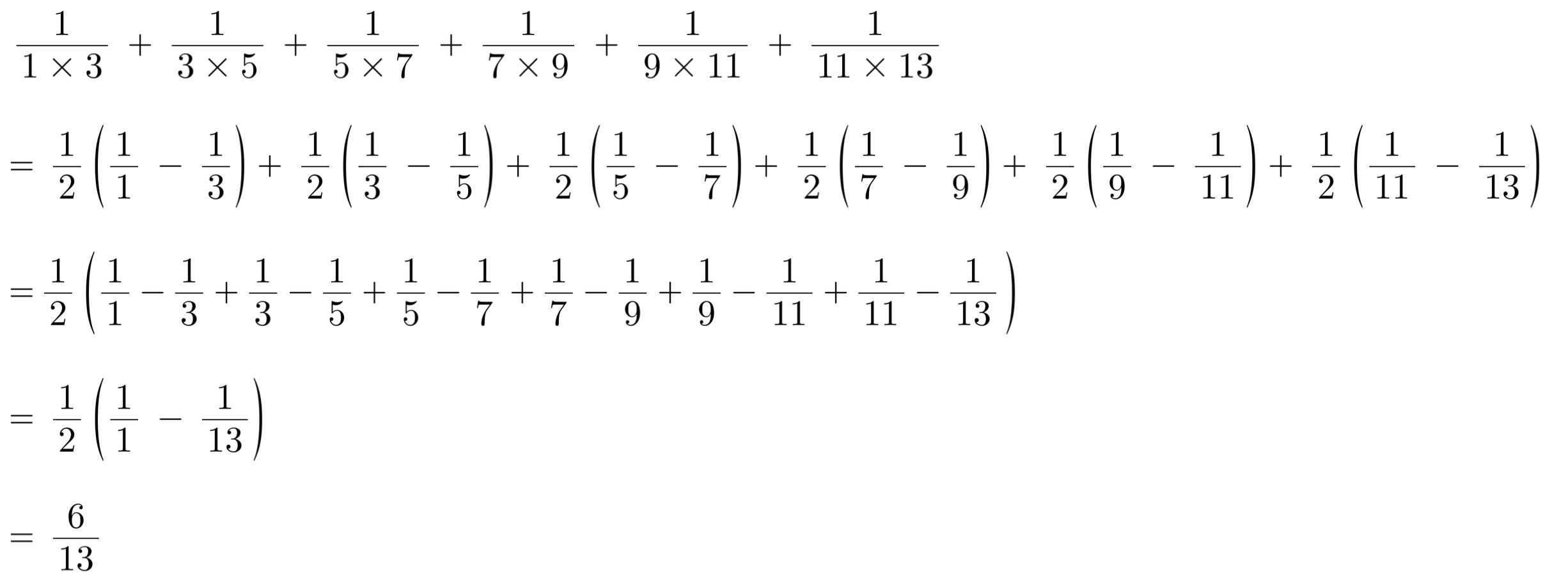
ポイント
実はこの計算は部分分数分解と呼ばれる計算方法を使っています。
中堅以上の中学の入試、高校数学ではよく見かける内容です。
しかし、中学受験を経験したことの無い公立あがりの生徒は解いたことが無い問題でしょう。
ただ、解いた事が無いといっても内容は分数の計算であり、要はテクニック的な事なのです。
よって、中学教科書に載ってないとか文句を言ってもしょうがないです。
内容的には小学校の内容なのですから。
ここで重要なのは、やった経験が無いだろうから(ア)の問題が存在しているという事。
いわゆる気づきの問題です。
(イ)に活用してね!と出題者の親切があるわけです。
そこを読み取れば経験が無くても解けるでしょうし、そういう事が出来る生徒を学校が望んでいるって事。
(イ)を無理やり通分するようではダメダメですよ。
無理やり通分して計算するくらいなら、いったん飛ばして次に行く方が賢いですね。
通分は最終手段です!
示唆
さて、冒頭で示唆に富んでいるとお伝えしました。
この問題は高校入試ではあまり見かけなかった問題ですが、その内容は小学校の内容です。
これからの入試ではこのような事例が頻繁に起こり得ると僕は考えています。
2020年大学入試改革に合わせた変化だと考えられるので、この流れは止まりません。
思考型の問題として使われそうな題材。
特に中学受験の内容や中学生でも理解できる高校範囲の内容などは狙い目となるでしょう。
先に対策するのがおススメです!
まとめ
今回は大阪以外の問題にも目を向けてみました。
各都道府県で入試の問題にも変化が出ているようです。
高大接続の流れに合わせた中高接続の流れを乗り切りましょう!

